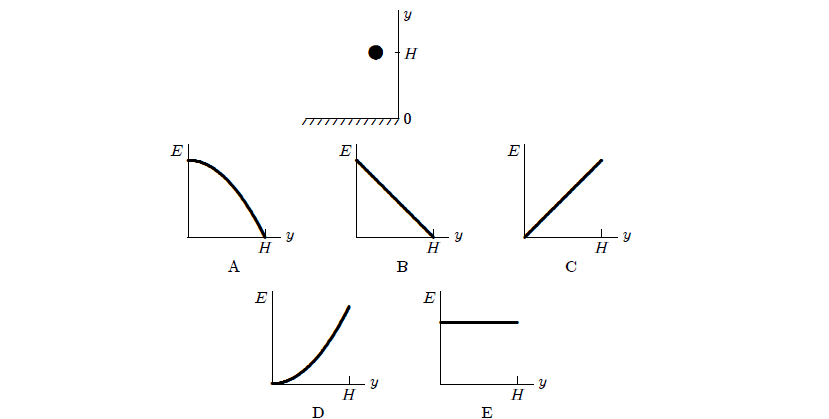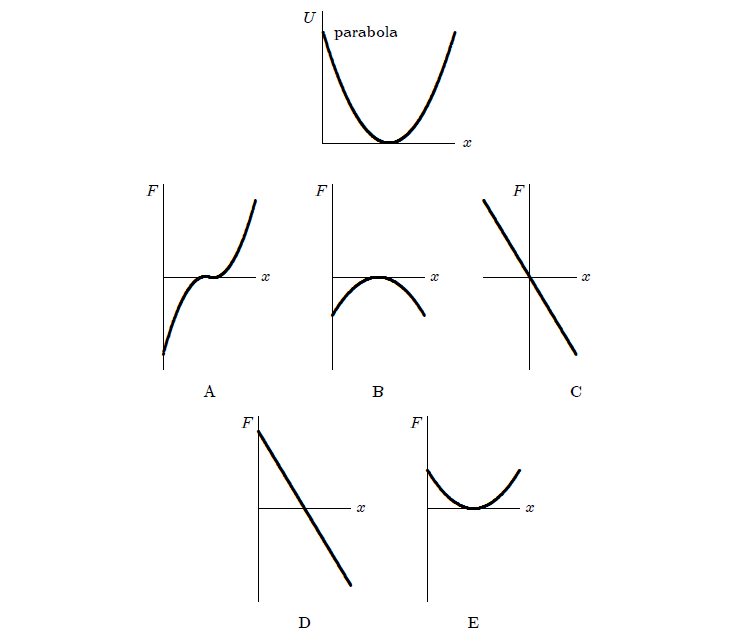Medizinishe Physick und Biophysick
Kursbeschreibung
1.Abteilung: ABTEILUNG FÜR BIOPHYSIK UND RADIOLOGIE
2. Thema: MEDIZINISCHE PHYSIK UND BIOPHYSIK
3. Kursleiter: Doc. dr. sc. Hrvoje Brkić
4. Studienjahr: 2021/22
5. Studienjahr: I.
6.ECTS-Punkte: 6
Pflichtlektüre:
1. Physick fur mediziner
2. Literatur des Fachbereichs des Tages auf der Website des Fachbereichs: www.physics.mefos.hr und im Merlin-System
Ergänzende Literatur:
1. D. C. Giancoli: Physik: Prinzipien mit Anwendungen, 6. Auflage, Prentice Hall, Inc., 2004. ISBN: 0130606200.
2. G. Rontó, I. Tarján, L. Berkes, S. Györgyi: An Introduction to Biophysics with Medical Orientation, Akadémiai Kiadó, Budapest, 1999. ISBN: 9630576074.
FORMEN UND BEDINGUNGEN DER WISSENSBEURTEILUNG
Untersuchungsmethode:
Die Prüfung gliedert sich in vier Teile:
(1) Praktische Prüfung - Während des Unterrichts werden die Studierenden zwei praktische Übungen im Praktikum (1. Herde des Gebäudes im KBCO-Kreis) machen. Jede Übung wird mit maximal 3 Punkten bewertet. Die vier verbleibenden Übungen werden im E-Format durchgeführt, jede dieser Übungen wird mit maximal einem Punkt bewertet. Insgesamt bringen die Übungen maximal 10 Punkte.
(2) schriftliche Prüfung - 40 Multiple-Choice-Fragen
(3) Seminare
a) Aufgabe - Durchführung eines Seminars zu einer gegebenen Aufgabe - maximal 3 Punkte. Das Seminar wird nicht präsentiert, muss aber bis zum 21. Dezember um 21:00 Uhr an Ova e-mail adresa je zaštićena od spambota. Potrebno je omogućiti JavaScript da je vidite.
gesendet werden. Es müssen 3-5 A4-Seiten geschrieben werden, Schriftgröße 12, Zeilenabstand 1,5. Seminare im PDF-Format versenden. ALLE Seminare werden verglichen und die Übereinstimmung mit dem bereits vorhandenen Text höher als 50% wird mit -3 (drei negativen) Punkten bewertet.
b) Teilnahme an Lehrveranstaltungen während der Vorlesung - maximal 1 Punkt
c) Schriftliche Prüfungen während des Unterrichts - maximal 6 Punkte
Kriterium:
33-35 ausreichend (2)
36-41 gut (3)
42-50 sehr gut (4)
51-60 ausgezeichnet (5)
(4) mündliche Prüfung (auf Wunsch des Studierenden kann statt einer schriftlichen auch eine mündliche Prüfung beantragt werden).
BERATUNG: Während des Unterrichts eine Stunde vor und nach der Vorlesung, den Rest des Jahres Montag von 08:00 bis 10:00
Seminares:
RADIOAKTIVITÄT
1.1. Wie groß ist die Masse der Jodisotopenprobe 131I mit einer Aktivität von 3,7*109 Bq, wenn ihre Halbwertszeit 8,4 Tage beträgt?
1. 2. Die gemessenen Werte der Aktivität einer radioaktiven Probe zu verschiedenen Zeiten sind in der Tabelle aufgeführt.
a) Wie ist die Halbwertszeit der Probe?
b) Wie wird die Aktivität der Probe nach 20 Stunden sein?
2. Eine Radonprobe 222Rn86 mit einem Volumen von 0,1 ml hat eine Temperatur von 27 ° C und einen Druck von 2026,5 hPa.
a) Wie hoch ist die Halbwertszeit von 222Rn86, wenn die Probe an einem Tag 8,12 * 1017 α-Partikel emittiert?
b) Wie viele α-Partikel werden während der Woche aus den Proben emittiert?
3. Zeigen Sie anhand eines Beispiels den Zusammenhang zwischen der elektronischen Konfiguration und den Quantenzahlen
4. Der Massenanteil von Kalium im menschlichen Körper beträgt 0,25%, und natürliches Kalium enthält 0,0117% des radioaktiven Isotops 40Ka, dessen Halbwertszeit 1,277 Milliarden Jahre beträgt. Bestimmen Sie die Gesamtzahl der 40Ka-Kerne im menschlichen Körper mit einer Masse von 40 kg und ihre Aktivität.
5. Die Absorption von Gammastrahlungen
MECHANIK
6. Analysieren Sie die Biomechanik des Anhebens einer Last vom Boden aus einer stehenden Position und aus einer Hockstellung.
7. Weltrekorde (für Männer) beim Kugelstoßen, Diskuswerfen und Speerwerfen sind 23,12 m, 74,08 m und 98,48 m. Die Massen dieser Körper sind: die Kugel 7,26 kg, der Diskus 2 kg und der Speer 800 g.
a) Berechnen Sie die Arbeit, die erforderlich ist, um den Rekord zu erreichen, wenn der Winkel, der durch die Richtung der Anfangsgeschwindigkeit zur Horizontalen geschlossen wird, 45 ° beträgt und die Höhe des Athleten 1,8 m ist.
b) Wenn die Auswurfzeit durchschnittlich 0,5 s beträgt, berechnen Sie die entsprechenden Leistungen des Athleten. Können sie sie mit der Konstitution (Höhe) des Athleten verbinden?
9. Das Teilchen hat eine Masse von 0,11 g und befindet sich in einer 15 cm langen Eprouvette, die mit Flüssigkeit gefüllt ist. Die Widerstandskraft, mit der sich die Flüssigkeit entgegensetzt, beträgt 1.079 mN. a) Berechnen Sie wie lange es dauert bis das Teilchen durch Sedimentation auf den Boden der Eprouvette fällt; b) Berechnen Sie wie lange es dauert bis ein Teilchen auf den Boden einer Eprouvette fällt, indem Sie die Zentrifuge verwenden, die sich 100 Mal pro Minute dreht und einen Rotationsradius von 20 cm hat.
10. Ein 2 kg schwerer Körper ist mit einem Faden verbunden und dreht sich um einen Punkt in der vertikalen Ebene im Gravitationsfeld der Erde. Berechnen Sie die Differenz zwischen den Spannkräften des Fadens, wenn sich der Körper am höchsten und niedrigsten Punkt der Flugbahn befindet.
11. EXPERIMENT: Mohr-Westphalsche-Waage
12. EXPERIMENT: Zentrifuge
13. Praktische Übung: Kräfte an der schiefen Ebene und am Kran
14. Praktische Übung: Hebel
15. Archimedisches Gesetz (6.2., 6.6.)
16. Die harmonische Schwingung einer Kugel auf eine Feder wird durch die Gleichung x (t) = A sin ωt beschrieben. In einem Abstand von 5 cm von der Gleichgewichtsposition beträgt die Geschwindigkeit der Kugel 17,3 cm / s und die Beschleunigung -20 cm / s2.
a) Wie groß ist die Schwingungsamplitude der Kugel?
b) Wie lange ist die Periode in der die Kugel schwingt?
OPTIK
17. 1. Eine sehr dünne Schicht einer transparenten Substanz mit einem Brechungsindex n1, der kleiner als der Brechungsindex des Glases n2 ist, wird häufig auf Linsen und andere optische Körper aufgebracht, um die Reflexion des Lichts von ihrer Oberfläche zu verringern.
Bestimmen Sie die Mindestdicke einer solchen Schicht, die die Reflexion des zentralen Teils des Weißlichtspektrums verhindern würde. Das Licht fällt fast senkrecht zur dünnen Schicht und der Brechungsindex des verwendeten Mittels beträgt 1,3. Erklären Sie, warum das Kameraobjektiv hellviolett aussieht.
17. 2. Die Verschiebung eines Lichtstrahls durch eine 3 mm dicke planparallele Platte beträgt 2.517 mm. Was ist der Brechungsindex einer planparallelen Platte, wenn der Einfallswinkel des Lichtstrahls auf die planparallele Platte doppelt so groß ist wie der Winkel der ersten Brechung?
18. Der Ball befindet sich im Pool (Punkt A), an dessen Rand der Beobachter steht (Punkt B). Der Mindestabstand des Balls vom Rand des Pools beträgt 36 m (Punkt C), und der Beobachter muss zu diesem Punkt 42 m entlang des Randes gehen.
a) Wenn die Gehgeschwindigkeit entlang des Pools 1,5 m / s und die Schwimmgeschwindigkeit 0,9 m / s beträgt, finden Sie heraus, wie sich der Beobachter bewegen sollte, um von Punkt B nach Punkt A zu gelangen.
b) Wie viel (minimale) Zeit würde er dafür brauchen und wie viel Zeit würde er brauchen wenn er diagonal gehen würde (von B nach A)?
c) Lösen Sie das Problem mit dem Gesetz der geometrischen Optik.
19. 1. Welche Stärke der Brille benötigt ein weitsichtiger Rentner, um Gegenstände, die 25cm vom Auge entfernt sind, scharf zu sehen, wenn er ohne Brille die Gegenstände auf einer Entfernung weniger als 120cm vom Auge nicht scharf sehen kann. Die Brille befindet sich in einem Abstand von 2 cm vor dem Auge.
19. 2. Die Sammellinse liefert ein realistisches Bild andersrum und 14% reduziert. Wenn wir das Objektiv 20 cm näher an das Objekt bringen, wird das Bild virtuell, aufrecht und um 70% vergrößert. Bestimmen Sie die Stärke der Linse.
20. Ein Lichtstrahl fällt unter einem Einfallswinkel von 60 ° auf die Seitenfläche eines Glasprismas mit einem Brechungsindex von 1,5 in der Nähe seiner Spitze. Was ist der Ablenkungswinkel des Lichtstrahls, wenn der Spitzenwinkel des Prismas 55 ° beträgt?
21. EXPERIMENT: Optische Bank
a) Verwenden Sie eine optische Bank, um die Bilderzeugung einer Zerstreuungslinse zu zeigen
b) Erstellen Sie ein Bild, wenn das Objekt virtuell ist (mit zwei Linsen).
c) Die Sammellinse hat eine Brennweite von 10 cm. Das Objekt ist 20 cm von der Linse entfernt. Berechnen Sie, wo sich das Bild befindet. Wie wird das Bild sein? Überprüfen Sie es auf der optischen Bank.
d) Konstruieren Sie ein Mikroskop mithilfe der optischen Bank.
22. Augenmodell, Augenfehler
THERMODYNAMIK
23. 1. Die Länge des Eisenstreifens bei 0 ° C beträgt 314,16 cm. Was ist die Mindesttemperatur, die erforderlich ist, um den Streifen zu erwärmen und das Rad mit einer Querschnittsfläche von 7900 cm2 vollständig abzudecken? Der lineare Ausdehnungskoeffizient des Eisens beträgt 1,2 · 10 & supmin; & sup5; K & supmin; ¹
23. 2. Der Sauerstoff mit einer Temperatur von 100 ° C und bei einem Druck von 105 Pa wird isotherm auf einen Druck von 1,5 × 10 5 Pa komprimiert. Auf welche Temperatur sollte das Gas abgekühlt werden, um den Druck wieder auf seinen Anfangswert zu bringen?
24. Wie viel Energie wird benötigt, um 1 kg Wasser von -53 ° C auf 223 ° C zu erwärmen?
25. 1. Bei einer Temperatur von 10,2 ° C schwimmt ein Körper mit einer Dichte von 0,88 g / cm3 in Öl dessen Dichte 0,9 cm3 beträgt. Der Körper beginnt bei der Temperatur von 68 ° C im Öl zu senken. Wie groß ist der Volumenausdehnungskoeffizient des Körpers, wenn der Volumenausdehnungskoeffizient des Öls 7 * 10-4 K-1 beträgt?
25. 2. EXPERIMENT: Gasgesetze (2 Studenten)
a) bestätigen Sie die Gasgesetze mit der Verwendung der gegebenen Apparatur
b) die Gesetze mit der Gaszustandsgleichung verbinden
26. 1. Im Kalorimeter befindet sich ein Eiswürfel mit einer Temperatur von 0 ° C. In das Kalorimeter werden 0,419 l Wasser bei 43 ° C gegossen. Die Gleichgewichtstemperatur beträgt 5 ° C . Bestimmen Sie die Anfangsmasse des Eiswürfels im Kalorimeter und die Zunahme der Entropie, bis das Gleichgewicht erreicht ist.
26. 2. EXPERIMENT: Kalorimeter
KONZEPTIONELLE AUFGABEN
27.1. Die Koordinaten des Objekts werden als Funktion der Zeit durch die Gleichung x = 7t - 3t2 angegeben, wobei x in Metern und t in Sekunden angegeben ist. Die Durchschnittsgeschwindigkeit des Objekts während des Intervalls t = 0 bis t = 4 s beträgt:
A. 5m/s
B. −5m/s
C. 11m/s
D. −11m/s
E. −14.5m/s
27.2. Der Ball befindet sich in einer Höhe H über dem Boden, wird fallen gelassen und fällt zu Boden. Wenn wir den Luftwiderstand ignorieren, welche der 5 Grafiken zeigt genau die mechanische Energie E des Erde-Ball Systems als Funktion der Höhe y des Balls?
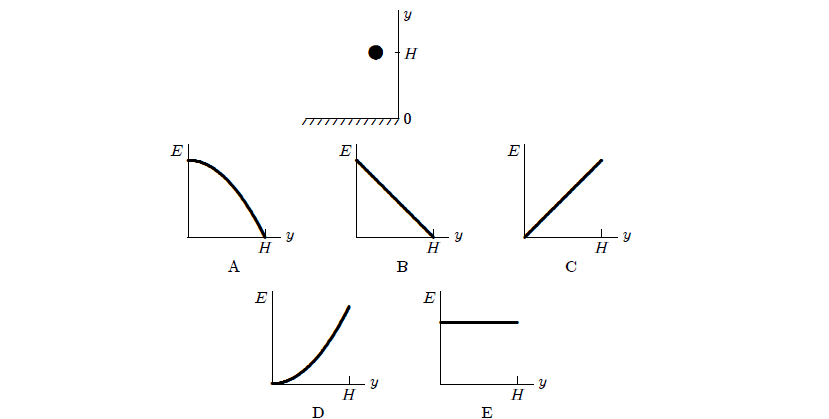
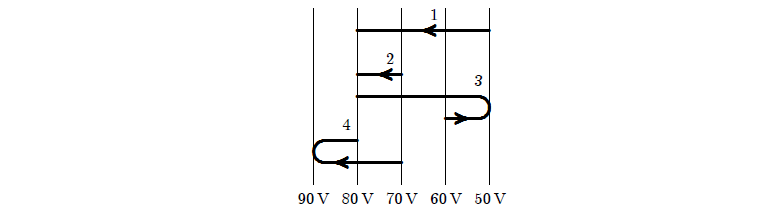
28.1. Das Elektron bewegt sich von einer Äquipotentialfläche zur anderen längs der vier Pfaden, wie in den Skizzen gezeigt. Ordnen Sie die Pfaden nach der Arbeit des elektrischen Feldes vom kleinsten zum größten.
A. 1, 2, 3, 4
B. 4, 3, 2, 1
C. 1, 3, 4 und 2 gleichermaßen
D. 4 und 2 gleichermaßen, dann 3, dann 1
E. 4, 3, 1, 2
28.2. Schließen Sie einen Widerstand (R), eine Spule (L) und zwei Glühbirnen (1 und 2) wie gezeigt an die Wechselstromquelle (Niederfrequenz) an. Was passiert mit der Reihenfolge, in der die Glühbirnen angezündet werden, wenn wir einen Eisenkern in eine Spule stecken? Erklären Sie die Antwort in Worten.
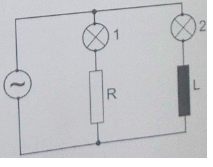
A. Sie brennen gleichzeitig
B. Glühbirne 1 leuchtet vor der Glühbirne 2
C. Die Kleinlichter sind die ganze Zeit an
D. Die Kleinlichter leuchten überhaupt nicht
E. Nichts des oben Genannten
29.1. Der erste Graph zeigt die potentielle Energie U (x) für eine Partikel, die sich entlang der x-Achse bewegt. Welcher der übriggebliebenen fünf Graphen gibt die auf die Partikel wirkende Kraft F korrekt an?
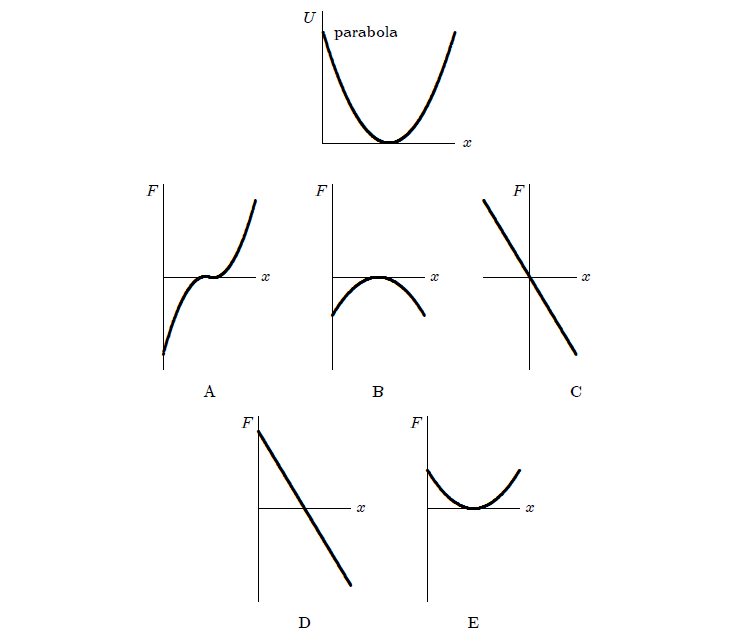
29.2. Auf dem Mond befinden sich eine normale Personenwaage und eine Präzisionswaage (mit Zweigen). Welche Waage zeigt das genaue Gewicht eines 1-kg-Gewichts an?
30.1. Wenn λ die Wellenlänge jeder Komponente der sinusförmigen Wanderwelle ist, aus der die stehende Welle besteht, beträgt der Abstand zwischen benachbarten Knoten:
A. λ/4
B. λ/2
C. 3λ/4
D. λ
E. 2λ
30.2. Drei identische Flaschen auf dem Bild sind unterschiedlich mit Wasser gefüllt. Wenn wir jede Flasche mit einem Holzhammer schlagen, welche Flasche gibt den höchsten Ton ab?

Praktische Ubungen:
1. Elektrische Stromkreise
2. Mikroskop
3. Viskosität von Flüßigkeiten
4. Luftfeuchtigkeit
5. Die Oberflächenspannung von Flüßigkeiten
6. Ultraschall