Seminari medicina
R A D I O A K T I V N O S T
1.1. Kolika je masa uzorka izotopa joda 131I aktivnosti 3,7*109 Bq ako mu je vrijeme poluraspada 8,4 dana?
1. 2. Mjerene vrijednosti aktivnosti nekog radioaktivnog uzorka u različitim vremenima prikazane su tablicom.
a) Koliko je vrijeme poluraspada uzorka?
b) Kolika će biti aktivnost uzorka nakon 20 h?
|
t/h |
0 |
4 |
8 |
|
A*1011Bq |
A0 |
28,94 |
8,93 |
2. Uzorak radona 222Rn86 zapremine 0,1ml nalazi se na temperaturi 27°C i tlaku 2026,5 hPa.
a) koliko je vrijeme poluraspada 222Rn86 ako uzorak u jednom danu emitira 8,12*1017 α-čestica;
b) koliko će α-čestica biti emitirano iz uzoraka tijekom tjedan dana?
3. Na primjeru pokaži vezu između elektronske konfiguracije i kvantnih brojeva
4. Maseni udio kalija u ljudskom tijelu iznosi 0,25%, a prirodni kalij sadrži 0,0117% radioaktivnog izotopa 40Ka čije je vrijeme poluraspada 1,277 milijardi godina. odredi ukupan broj jezgri 40Ka u ljudskom tijelu mase 40 kg i njegovu aktivnost.
M E H A N I K A
6. Analiziraj biomehaniku podizanja tereta s poda iz stajaćeg položaja i iz čučnja.
7. Svjetski rekordi (za muškarce) u bacanju kugle, diska i koplja iznose 23,12 m, 74,08 m i 98,48 m. Mase tih tijela iznose: kugla 7,26 kg disk 2 kg i koplje 800 g.
a) Izračunaj rad koji je potrebno izvršiti da bi se postigao rekord, ako je kut što ga zatvara pravac početne brzine prema horizontali 45°, a visina sportaša 1,8 m
b) Ako je vrijeme izbačaja prosječno 0,5 s, izračunaj odgovarajuće snage sportaša. Mogu li se one povezati sa konstitucijom (visinom) sportaša.
9. Čestica ima masu 0,11 g, i nalazi se u epruveti duljine 15 cm, koja je ispunjena tekućinom. Sila otpora kojom se tekućina suprotstavlja iznosi 1.079 mN. a) izračunaj koliko je vrijeme potrebno čestici da sedimentacijom padne da dno epruvete; b) izračunaj koliko je vrijeme potrebno čestici da padne na dno epruvete koristeći centrifugu koja se okreće 100 puta u minuti, i ima radijus vrtnje 20 cm?
10. Tijelo mase 2 kg vezano je koncem i rotira oko jedne točke u vertikalnoj ravnini u polju Zemljine teže. Izračunati razliku među silama zatezanja konca kada se tijelo nalazi u najvišoj i najnižoj točki putanje
11. POKUS: Mohr-Westphalova vaga
12. POKUS: Centrifuga
13. Praktična vježba: Sile na kosini i dizalici
14. Praktična vježba: Poluga
15. Arhimedov zakon (6.2., 6.6.)
16. Harmonijsko titranje kuglice na opruzi opisano je jednadžbom x(t)=A sin ωt. Na udaljenosti 5 cm od položaja ravnoteže brzina kuglice je 17,3 cm/s, a ubrzanje -20 cm/s2.
a) Kolika je amplituda titranja kuglice?
b) Koliki je period titranja kuglice?
O P T I K A
17. 1. Na leće i druga optička tijela često se stavlja vrlo tanki sloj prozirne tvari indeksa loma n1 manjeg od indeksa loma stakla n2 da bi se smanjila refleksija svjetlosti s njihove površine. Odredite minimalnu debljinu takvog sloja koji bi spriječio refleksiju središnjeg dijela spektra bijele svijetlosti. Svjetlost upada gotovo okomito na tanki sloj, a indeks loma upotrebljenog sredstva iznosi 1,3. Objasnite zašto leće fotoaparata izgledaju sviijetlo ljubičasto.
17. 2. Pomak zrake svjetlosti pri prolasku kroz planparalelnu ploču debljine 3 mm je 2,517 mm. Koliki je indeks loma planparalelne ploče ako je kut upada zrake svjetlosti na planparalenu ploču dva puta veći od kuta prvog loma?
18. Lopta se nalazi u bazenu (točka A) uz čiji rub stoji promatrač (točka B). Najmanje udaljenost lopte od ruba bazena je 36 m (točka C), a promatrač do te točke mora hodati uz rub 42 m.
a) Ako je brzina hodanja uz rub bazena 1,5 m/s, a brzina plivanja 0,9 m/s, nađi na koji način se treba gibati promatrač da bi iz točke B došao u točku A.
b) Koliko (minimalno) vrijeme bi mu za to bilo potrebno, a koliko vremena bi mu trebalo kada bi išao dijagonalno (iz B u A)?
c) Riješi zadatak pomoću zakona geometrijske optike.
19. 1. Kolika je jakost naočala potrebna da dalekovidni umirovljenik oštro vidi predmete udaljene 25 cm od oka ako on bez naočala ne vidi oštro predmete a udaljenosti manjoj od 120 cm od oka? Naočale se nalaze na udaljenosti 2 cm ispred oka.
19. 2.Sabirna leća daje realnu sliku obrnutu i 14% umanjenu. Ako leću približimo predmetu za 20 cm slika postane virtualna, uspravna i 70% uvećana. Odredi jakost leće.
20. Zraka svjetlosti pada pod kutom upada 60° na bočnu plohu staklene prizme indeksa loma 1,5 blizu njenog vrha. Koliki je kut devijacije zrake svijetlosti ako je vršni kut prizme 55°?
21. POKUS: Optička klupa
a) pomoću optičke klupe prikaži stvaranje slike kod divergentne leće
b) konstruiraj sliku kada je predmet virtualan (koristeći dvije leće)
c) konvergentna leća ima žarišnu daljinu 10 cm. Predmet se od leće nalazi 20 cm. Izračunaj gdje se nalazi slika. Kakva će slika biti? Provjeri to na optičkoj klupi.
d) konstruiraj mikroskop pomoću optičke klupe
T E R M O D I N A M I K A
24. 1. Duljina željezne trake pri temperaturi 0°C je 314,16 cm. Na koliku je najmanju temperaturu potrebno zagrijati traku da bi se njome u potpunosti obuhvatio kotač površine presjeka 7900 cm2? Koeficijent linearnog širenja željeza je 1,2*10-5 K-1
24. 2. Kisik temperature 100 °C pri tlaku 105 Pa izotermno stlačimo do tlaka 1,5*105 Pa. Do koje temperature treba ohladiti plin da bi se tlak vratio na svoju početnu vrijednost?
25. Kolika je energija potrebna da se 1 kg vode zagrije od -53°C do 223°C?
26. 1. Pri temperaturi 10,2°C tijelo gustoće 0,88 g/cm3 pliva u ulju gustoće 0,9 cm3, a pri temperaturi 68°C tijelo počne tonuti u ulje. Koliki je koeficijent volumnog širenja tijela ako je koeficijent volumnog širenja ulja 7*10-4 K-1?
26. 2. POKUS: Plinski zakoni (2 studenta)
a) koristeći danu aparaturu potvrdi plinske zakone
b) povezati zakone s jednadžbom stanja plina
27. 1. U kalorimetru se nalazi kocka leda temperature 0°C. U kalorimetar se ulije 0,419 l vode temperature 43°C. Ravnotežna temperatura uspostavi se na 5°C. Odredi početnu masu leda u kalorimetru i porast entropije do postizanja racvnoteže.
27. 2. POKUS: Kalorimetar
KONCEPTUALNI ZADATCI
29.1. Koordinate objekta dane su kao funkcija vremena jednadžbom x = 7t − 3t2, gdje je x u metrima a t u sekundama. Prosječna brzina objekta tijekom intervala t = 0 do t = 4 s je:
A. 5m/s
B. −5m/s
C. 11m/s
D. −11m/s
E. −14.5m/s
29. 2. Lopta se nalazi na visini H iznad podloge je puštena i pada na tlo. Ako zanemarimo otpor zraka, koji od 5 grafova točno prikazuje mehaničku energiju E sustava Zemlja-lopta kao funkciju visine y lopte?
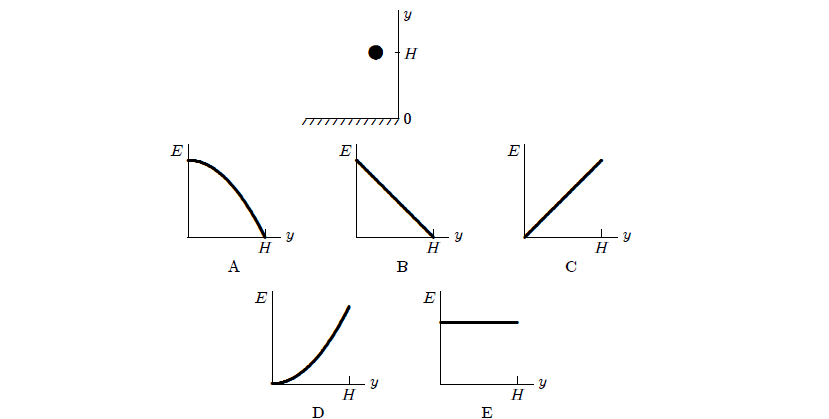
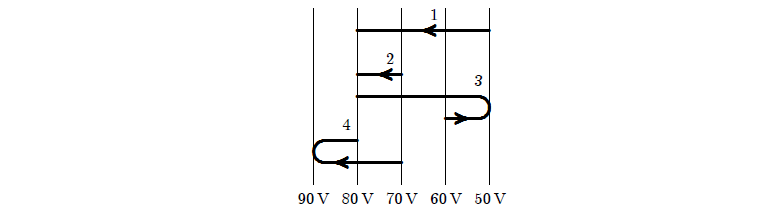
30. 1. Elektron kreće sa jedne ekvipotencijalne plohe na drugu duž četiri putanje prikazane na skici. Rangiraj puteve prema radu koje izvede električno polje od najmanjeg prema najvećem.
A. 1, 2, 3, 4
B. 4, 3, 2, 1
C. 1, 3, 4 i 2 jednako
D. 4 i 2 jednako, zatim 3, pa 1
E. 4, 3, 1, 2
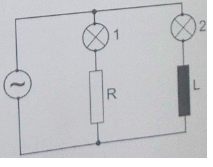
30. 2. Na izvor izmjeničnog napona (niske frekvencije) priključimo otpornik (R), zavojnicu (L) i dvije žarulje (1 i 2) kao na slici. Kad stavimo u zavojnicu željeznu jezgru što se događa s redoslijedom paljenja žaruljica? Odgovor obrazložite riječima.
A. Pale se istovremeno
B. Žarulja 1 pali se prije žarulje 2
C. Žaruljice cijelo vrijeme svijetle
D. Žaruljice uopće ne svijetle
E. Ništa od navedenog
31. 1. Prvi graf pokazuje potencijalnu energiju U(x) za česticu koja se kreće duž x osi. Koji od preostalih pet grafova ispravno daje silu F koja djeluje na česticu?
31. 2. Na Mjesecu se nalaze sobna vaga i „precizna vaga“ (s krakovima). Koja će vaga prikazati točnu masu utega mase 1kg. 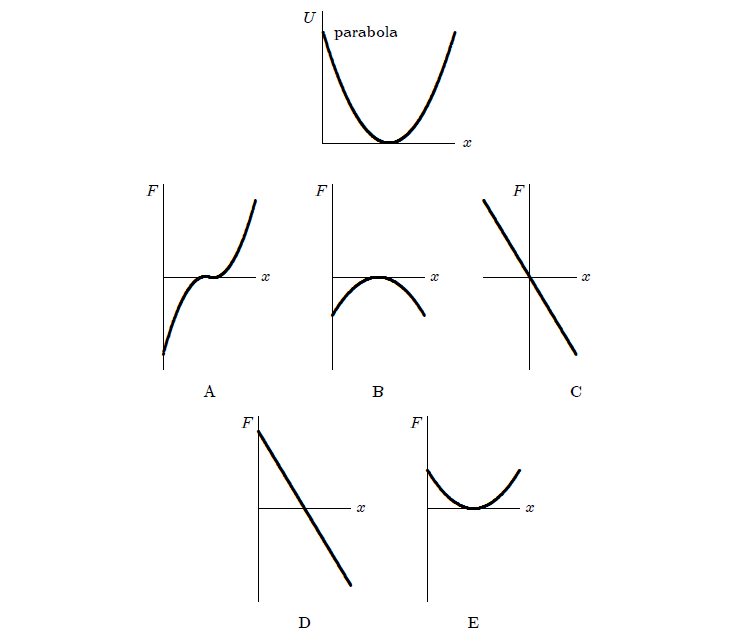
32. 1. Ako je λ valna duljina svake komponente sinusoidalnog putujućeg vala koji čini stojni val, udaljenost između susjednih čvorova iznosi:
A. λ/4
B. λ/2
C. 3λ/4
D. λ
E. 2λ
32. 2. Tri su jednake boce na slici različito napunjene vodom. Kada udarimo batićem po svakoj boci, koja će boca ispuštati najviši ton?

33. 1. Na grafovima ispod prikazana je veličina sile na česticu poteza uz pozitivne x osi od nastanka do x = x1. Sila je paralelna s x osi i konzervativna. Maksimum magnitude F1 ima istu vrijednost za sve grafove. Poredaj grafove u skladu s promjenom potencijalne energije povezana sa silom , od najmanje ( ili najnegativniji ) do najveće ( ili najpozitivnija ) .
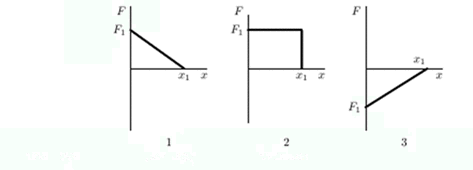
A. 1, 2, 3
B. 1, 3, 2
C. 2, 3, 1
D. 3, 2, 1
E. 2, 1, 3
33. 2. Jednostavni harmonijski oscilator se sastoji od čestica mase m i idealne opruge s konatantom k. Čestica oscilira kao što je prikazano na slici (i) s periodom T. Ako je opruga prepolovljena, a čestica je ostala ista, kao što je prikazano na slici (ii), period će biti:
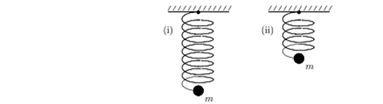
A. 2T
B. √2 T
C. T/√2
D. T
E. T/2
34. 1. Elektron i proton imaju isti impuls. Kakva je frekvencija i valna duljina elektrona u usporedbi s protonom?
A. kraća valna duljina i veća frekvencija
B. veća valna duljina i veća vrekvencija
C. Kraća valna duljina i ista frekvencija
D. Veća valna duljina i ista frekvencija
E. Kraća valna duljina i manja vrekvencija
34. 2. Tri identične niti (X,Y,Z) su postavljene kako je prikazano. Kada uteg od 4 kg onjesimo na oprugu X, ona se produlji za 3 cm. Kada uteg od 6 kg objesimo na Y, ukupno produljenje iznosi:
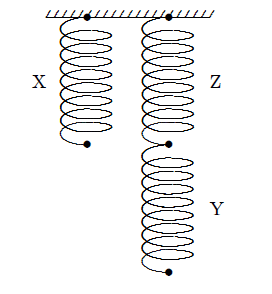
A. 2.0 cm
B. 4.0 cm
C. 4.5 cm
D. 6.0 cm
E. 9.0 cm
35. 1. Čamac pluta na vodi.U čamcu se nalaze 3 olovne kuglice. Nakon što kuglice ispadnu u vodu, što će se dogoditi s razinom vode?
35. 2. Koordinate objekta dane su kao funkcija vremena jednadžbom x = 4 t2 – 3 t3, gdje je x u metrima a t u sekundama. Prosječna akceleracija objekta tijekom intervala t = 0 do t = 2 s je?
36. 1. Dva termometra se nalaze u sobi i mjere temperaturu 21°C. Krpu namočimo u alkohol iste temperature pa ju zamotamo oko jednog termometra. Hoće li termometri pokazivati istu temperaturu nakon nekog vremena? (Dovoljno je sačekati 30s)
36. 2. Količina idealnog plina je komprimirana na polovicu svog početnog volumena. Proces može biti adijabatski, izoterman ili izobaran. Rangiraj ova tri procesa prema iznosu rada koji je potrebno izvesti od najnižeg prema najvišem:
A. adijabatski, izotermni, izobarni
B. adijabatski, izobarni, izotermni
C. izotermni, adijabatski, izobarni
D. Izobarni, adijabatski, izotermni
E. Izobarni, izotermni, adijabatski
37.1. Kada je sklopka S otvorena, ampermetar u krugu pokazuja 2.0 A. Koliko pokazuje ampermetar ako je sklopka S zatvorena?
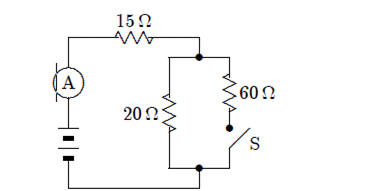
A. lagano povećanje
B. ostaje isto
C. lagano se smanji
D. udvostruči se
E. prepolovi se
37. 2. Možemo li električki nabijenim staklenim štapom djelovati na magnetnu iglu kompasa?
38. 1. Osoba puše preko jednog kraka U-cijevi djelomično popunjene s vodom. Voda će se u tom kraku:
A. lagano podići
B. lagano spustiti
C. ostati na istoj visini
D. rasti ako je puhanje sporo, a padati ako je jako
E. rasti ako je puhanje jako, a padati ako je sporo
38. 2. Dvije nenabijene metalne sfere, L i M su u kontaktu. Negativno nabijen štap donešen je u blizinu sfere L, ali nije dotaknuo sfere. Ako dvije svere lagano razdvojimo, i nakon toga povučemo štap što će se dogoditi?
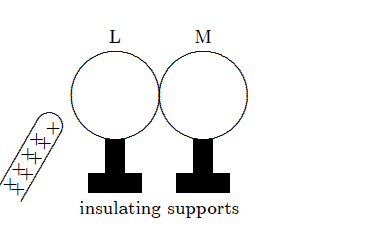
A. obje su sfere neutralne,
B. obje su sfere pozitivne
C. obje su sfere negativne
D. L je negativna, a M je pozitivna
E. L pozitivna, a M je negativna
39. 1. Dva utega su povezana preko niti i koloture kao što je prikazano na slici. Ako pretpostavimo da kolotura i nit nemaju masu, akceleracija svakog od utega iznosi:
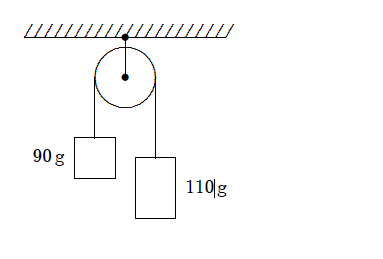
A. 0.049 m/s2
B. 0.020 m/s2
C. 0.0098 m/s2
D. 0.54 m/s2
E. 0.98 m/s2
39. 2. Tri knjige (X, Y, i Z) stoje na stolu kao na slici. Težina svake knjige je naznačena. Kolika je sila koja djeluje na knjugu Y?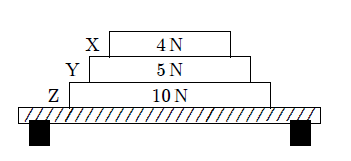
A. 4N dolje
B. 5N gore
C. 9N dolje
D. 0
E. ništa od ponuđenog nije točno
40. 1. Hladnjak se nalazi u termički izoliranoj sobi. otvorimo hladnjak i pustimo ga da radi 24h. Što će se dogoditi s temperaturom u sobi?
A. povećati se prema i. zakonu termodinamike
B. smanjiti se prema I. zakonu termodinamike
C. povećati se prema II. zakonu termodinamike
D. smanjiti se prema II. zakonu termodinamike
40. 2. Dva putujuća vala y1 = A sin [k (x−vt) ] i y2 = A sin [k (x+vt) ] su superponirani na istom užetu Udaljenost između susjednih čvorova je:
A. vt/π
B. vt/2π
C. π/2k
D. π/k
E. 2π/k
41. Struktura i mehanička svojstva stomatoliških materijala. Defekti. Dislokacije.
42. Most duljine 3 cm postavljen je na tri kutnjaka, a ima masu 10 g. Prvi zub može podnjeti silu od maksimalno 10 N. Izračunaj silu koju podnosi drugi zub ako je sila kojom predmet pritišče most na na udaljenosti 2.5 cm od drugog zuba 3 N.
43. U ustima koja su otvorena pod kutem od 30° se nalazi komad bombona. Udaljenost od zgloba čeljusti do sjekutića (gdje se nalazi i bombon) iznosi 10 cm. Izračunaj silu ugriza ako je krak sile mišića 6 cm, a sila mišića iznosi 5 N.
Način ocjenjivanja seminarskih zadataka
